(SPLDV)
A.
Pengertian
persamaan linear dua variabel (PLDV)
Persamaan linear dua variabel ialah persamaan yang
mengandung dua variabel dimanapangkat/derajat tiap-tiap variabelnya sama dengan
satu.
Bentuk Umum PLDV :
ax + by = c
x dan y disebut variable
B.
Sistem persamaan linear dua variable
(SPLDV)
Sistem persamaan linear dua variabel atau dalam
matematika biasa disingkat SPLDV adalah suatu persamaan matematika yang terdiri
atas dua persamaan linear, yang masing-masing bervariabel dua, misalnya
variabel x dan variabel y.
Ciri-ciri SPLDV:
· Sudah jelas terdiri dari 2 variabel
· Kedua variabel pada SPLDV hanya memiliki derajat satu atau berpangkat
satu.
· Menggunakan relasi tanda sama dengan (=)
· Tidak terdapat perkalian variabel dalam setiap persamaannya.
Berikut ini adalah langkah – langkah untuk menyelesaikan masalah dengan
menggunakan SPLDV:
1.
Mengganti setiap besaran yang
terdapat dalam suatu masalah dengan variabel.
2. Membuat model Matematika dari masalah
tersebut. Model matematika ini dirumuskan mengikuti bentuk umum dari SPLDV.
3. Mencari solusi dari model
permasalahan dengan menggunakan metode penyelesaian SPLDV.
Contoh:
Adi membeli 3 buah buku dan 2 buah pensil di sebuah toko seharga Rp.
13.000,00. Beni membeli 1 buah buku dan 1 buah pensil seharga Rp. 5.000,00.
Mereka lupa menanyakan harga masing – masing barang tersebut. Bagaimana cara
mengetahui harga buku dan pensil tanpa kembali ke toko dan bertanya kepada
penjual?
Jawab:
Permasalahan di atas adalah salah satu masalah dalam kehidupan sehari –
hari yang membutuhkan penggunaan Matematika dalam penyelesaiannya. Masalah di
atas dapat diselesaikan menggunakan SPLDV dengan langkah – langkah berikut:
Langkah
1 (mengganti setiap besaran dengan variabel)
Misalkan harga 1 buah buku dinotasikan dan harga 1 buah pensil dinotasikan dengan
.
Langkah
2 (membuat model Matematika)
- Harga 3 buah buku dan 2 buah pensil adalah Rp. 13.000,00. Pernyataan tersebut dapat dimodelkan menjadi
.
- Harga 1 buah buku dan 1 buah pensil adalah Rp. 5.000,00. Pernyataan tersebut dapat dimodelkan menjadi
.
Sehingga, model Matematika dari permasalahan di atas adalah:
Langkah
3 (mencari solusi dari model Matematika menggunakan metode penyelesaian SPLDV)
Untuk mencari solusi dari model Matematika yang telah dibuat dengan
menggunakan metode penyelesaian SPLDV akan dijelaskan pada materi di bawah ini.
C. Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV)
Terdapat
beberapa metode untuk menyelesaikan Sistem Persamaan Linear Dua Variabel
(SPLDV), diantaranya:
Metode Eliminasi
Penyelesaian
Sistem Persamaan Linear Dua Variabel (SPLDV) dengan menggunakan metode
eliminasi dilakukan dengan cara menghilangkan (mengeliminasi) salah satu
variabel dari sistem persamaan tersebut. Jika variabel dalam suatu SPLDV
adalah dan maka untuk
menentukan nilai dari variabel kita harus
mengeliminasi variabel terlebih dahulu.
Begitupun sebaliknya.
Contoh:
Tentukan himpunan penyelesaian dari sistem persamaan
dan
menggunakan metode eliminasi!
Jawab:
Langkah 1 (mencari nilai variabel dengan mengeliminasi variabel
):
Metode Subtitusi
Metode substitusi adalah salah satu metode untuk menyelesaikan Sistem Persamaan Linear Dua Variabel (SPLDV) dengan cara menggantikan satu variabel dengan variabel dari persamaan yang lain.
Contoh:
Tentukan himpunan penyelesaian dari sistem persamaan dan
menggunakan metode subtitusi!
Jawab:
Persamaan ekuivalen dengan persamaan
. Dengan menyubtitusi persamaan
ke persamaan
, maka diperoleh:
Kemudian untuk memperoleh nilai , subtitusikan nilai
ke persamaan
, sehingga diperoleh:
Jadi, himpunan penyelesaiannya adalah .
Metode Gabungan
Metode gabungan adalah salah satu metode untuk menyelesaikan Sistem Persamaan Linear Dua Variabel dengan cara menggabungkan metode eliminasi dengan metode subtitusi.
Contoh:
Tentukan himpunan penyelesaian dari sistem persamaan dan
menggunakan metode gabungan!
Jawab:
Langkah 1 (mencari nilai variabel dengan metode eliminasi):
Langkah 2 (subtitusikan nilai ke persamaan
):

Setelah mempelajari materi di atas
silahkan kerjakan soal berikut ini
SALAM SEMANGAT SELALU!!

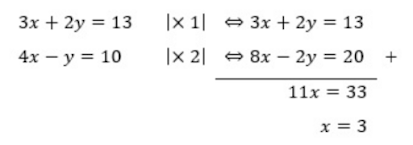







Tidak ada komentar:
Posting Komentar