Segi Empat dan Segi Tiga

BANGUN DATAR SEGI EMPAT DAN SEGI TIGA

Sifat bangun Datar Segi Empat dan Segi Tiga

Persegi

Persegi merupakan suatu bangun datar 2 dimensi yang terbentuk oleh 4 buah rusuk dengan memiliki ukuran sama panjang serta memiliki 4 buah sudut siku – siku.Persegi juga bisa kita sebut sebagai bangun datar yang mempunyai sisi sisi sama panjang serta sudut sudut sama besar.

Sifat Persegi

1. Seluruh sisi-sisinya memiliki ukuran panjang yang sama serta seuruh sisinya berhadapan sejajar.
2. Masing-masing sudut yang dimilikinya adalah sudut siku-siku.
3. Memiliki dua diagonal dengan ukuran panjang yang sama sama serta berpotongan di tengah-tengah dan membentuk sudut siku-siku.
4. Pada masing-masing sudutnya di bagi dua sama besarnya oleh diagonalnya.
5. Memiliki empat buah sumbu simetri.

Rumus Persegi

Rumus luas persegi, yaitu:

L = S x S

Rumus keliling persegi, yaitu:

K = S + S + S + S ataupun K = 4 x S

Keterangan:

L:    Luas
K:   Keliling
S:   Sisi

Persegi Panjang

Persegi panjang meurpakan suatu bangun datar 2 dimensi yang terbentuk oleh 2 buah pasang rusuk yang panjang serta sejajar dan memiliki 4 buah sudut siku – siku.

Sifat Persegi Panjang

1. Masing-masing sisi-sisi yang berhadapan memiliki ukuran sama panjang dan juga sejajar.
2. Seluruh sudutnya merupakan sudut siku-siku.
3. Mempunyai dua buah diagonal yang sama panjang serta saling berpotongan di titik pusat bangun persegi panjang. Titik tersebut adalah membagi dua bagian diagonal dengan ukuran sama panjang.
4. Mempunyai dua buah sumbu simetri yakni sumbu vertikal dan juga sumbu horizontal.

Rumus Persegi Panjang

Rumus luas persegi panjang, yaitu:

L = p x l

Rumus keliling persegi panjang, yaitu:

K = 2 x (p + l)

Keterangan:

L:Luas
K:Keliling
p:panjang
l: lebar

Jajar genjang

Pengertian dari jajar genjang sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk atas 2 buah pasang rusuk yang di mana pada masing – masing nya memiliki ukuran sama panjang serta sejajar dengan pasangan nya.

Kemudian jajar genjang memiliki 2 buah pasang sudut siku – siku yang di mana pada masing – masing sudutnya sama besar dengan sudut di depan nya.

Sifat Bangun Datar Jajar genjang

Sifat pada Jajar Genjang tidak memiliki simetri lipat.

1. Jajar Genjang memiliki simetri putar tingkat dua.
2. Sudut Jajar Genjang yang berhadapan memiliki ukuran yang sama besar.
3. Jajar Genjang memiliki 4 sisi serta 4 sisi sudut.
4. Diagonal yang dimilikinya memiliki panjang yang tidak sama.
5. Jajar Genjang memiliki 2 Pasang Sisi yang sejajar serta sama panjang.
6. Jajar Genjang memiliki 2 buah sudut tumpul dan 2 buah sudut lancip.

Rumus yang ada pada Bangun Datar Jajar genjang

Keliling = 2 × (a + b)

Luas (L) = a × t

Sisi Alas (a) a = (K ÷ 2) – b

Sisi Sisi Miring (b) a = (K ÷ 2) – a

t diketahui L t = L ÷ a

a diketahui L a = L ÷ t

Contoh Soal

Perhatikanlah gambar jajaran genjang ABCD di bawah ini!

bangun datar persegi

Panjang BC = DA = 8 cm.

Pertanyaan:

a. Hitunglah luas jajaran genjang ABCD, merupakan:

b. Hitunglah keliling jajaran genjang ABCD, merupakan:
= 56 cm2

Jawab:

a. Luas jajaran genjang ABCD adalah = a x t, sehingga

= 8 cm x 7 cm

Jadi, luas jajaran genjang ABCD yaitu 56 cm2.

b. Keliling jajaran genjang ABCD adalah s + s + s + s, maka:

K = AB + BC + CD + DA, yakni :
K = 8 cm + 8 cm + 8 cm + 8 cm
= 32 cm.

Jadi, keliling jajaran genjang ABCD adalah 32 cm.

---

Trapesium

Pengertian dari trapesium sendiri merupakan suatu bangun datar 2 dimensi yang dibentuk dari 4 buah rusuk yang 2 buah di antaranya merupakan saling sejajar namun panjang nya tidak sama.

Tetapi terdapat juga trapesium yang rusuk ketiganya merupakan tegak lurus pada rusuk – rusuk sejajar nya yang biasa dikenal dengan sebutan trapesium siku – siku.

Sifat Bangun Datar Trapesium :

1. Trapesium adalah bangun datar dengan 4 sisi (quadrilateral).
2. Memiliki 2 sisi sejajar yang tidak sama panjang.
3. Memiliki 4 buah titik sudut.
4. Minimal pada bagun datar trapesium memiliki 1 titik sudut tumpul
5. Trapesium memiliki 1 simetri putar.

Rumus yang ada pada Bangun Datar Trapesium

 

Nama Rumus

Luas (L) rumus luas trapesium

Keliling (K) K = AB + BC + CD + DA

Tinggi (t) rumus tinggi trapesium

Sisi a (CD) rumus sisi trapesiumatau CD = Kll – AB – BC – AD

Sisi b (AB) rumus trapesiumatau AB = K – CD – BC – AD

Sisi AD AD = K – CD – BC – AB

Sisi BC BC = K – CD – AD – AB

Contoh soal:

Perhatikanlah bangun datar trapesium EFGH di bawah ini!

sifat bangun datar

Panjang EH = FG ialah 8 cm.

Pertanyaan:

a. Tentukanlah luas trapesium EFGH:
b. Tentukanlah keliling trapesium EFGH:

Jawab:

a. Luas trapesium EFGH adalah: ½ x (a + b) x t maka,

= ½ x (16cm + 6 cm) x 7 cm
= ½ x 22 cm x 7 cm
= 11cm x 7 cm
= 77 cm2

Jadi, luas trapesium EFGH di atas adalah 77 cm2.

b. Keliling trapesium EFGH memiliki rumus yaknni: s + s + s + s, maka:

K = EF + FG + GH + HE
K = 16 cm + 8 cm + 6 cm + 8 cm
= 38 cm.

Jadi, luas keliling trapesium EFGH di atas adalah 38 cm.

Layang – layang

Pengertian dari layang – layang sendiri merupakan suatu bangun datar 2 dimensi yang di bentuk oleh 2 buah segitiga sama kaki serta berbentuk segiempat di mana memiliki alas yang berhimpitan dan berbentuk menjadi suatu layang – layang.

Sifat Bangun Datar Layang – layang :

1. Layang-layang adalah suatu bangun datar dengan 4 sisi (quadrilateral).
2. Memiliki 2 pasangan sisi yang membentuk sudut yang berbeda.
3. Pasangan 1 merupakan sisi a dan b, membentuk sudut ∠ABC.
4. Pasangan 2 merupakan sisi c dan d, membentuk sudut ∠ADC.
5. Memiliki sepasang sudut yang saling berhadapan dengan besar ukuran yang sama.
6. Sudut ∠BAD serta ∠BCD saling berhadapan dan memiliki besar yang sama.
7. Memiliki 2 diagonal dengan panjang yang berbeda.
8. Diagonal layang-layang saling tegak lurus (90º).
9. Diagonal terpanjang adalah sumbu simetri layang-layang.
10. Layang-layang hanya mempunyai 1 sumbu simetri.

Rumus yang ada pada Bangun Datar Layang – layang

Nama Rumus

Luas (L) L = ½ × d1 × d2

Keliling (K) K = a + b + c + d

K = 2 × (a + c)

Diagonal 1 (d1) d1 = 2 × L ÷ d2

Diagonal 2 (d2) d2 = 2 × L ÷ d1

a atau b a = (½ × K) – c

c atau d c = (½ × Kll) – a

Contoh Soal

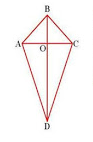
Perhatikan layang layang ABCD di bawah ini!

ciri ciri bangun datar

DiketahuI;

Panjang BC = panjang CD
Panjang AB = panjang AD

Pertanyaan:

a. Hitunglah luas layang layang ABCD!
b. Hitunglah keliling layang layang ABCD!

Jawab:
a. Luas layang-layang ABCD adalah = ½ x d1 x d2, sehingga

= ½ x AC x BD
= ½ x 30 cm x 15 cm
= 225 cm2

Jadi, luas layang layang ABCD tersebut yaitu 225 cm2.

b. Keliling dari layang-layang ABCD adalah: 2 x (x + y), sehingga

= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm

Jadi, keliling layang layang ABCD yaitu 68 cm.

---

Belah Ketupat

Belah Ketupat merupakan suatu bangun datar 2 dimensi yang dibentuk oleh 4 buah sisi dengan ukuran sama panjang serta memiliki 2 pasang sudut bukan siku-siku dengan sudut yang saling berhadapan memiliki besar sama. Dalam bahasa inggris, belah ketupat disebut sebagai rhombus.

Sifat Bangun Datar Belah Ketupat :

1. Keempat sisinya sama panjang.
2. Memiliki 2 diagonal yang saling tegak lurus.
3. Diagonal 1 (d1) dan diagonal 2 (d2) pada belah ketupat saling tegak lurus membentuk sudut siku-siku (90°).
4. Sudut yang saling berhadapan memiliki besar yang sama.
5. Pada belah ketupat sudut yang berhadapan memiliki besar yang sama. Ilustrasi di atas menunjukkan besar
6. sudut ∠ABC = ∠ADC dan ∠BAD = ∠BCD.
7. Besar pada keempat titik sudutnya 360º.
8. Memiliki 2 sumbu simetri yang di mana adalah diagonalnya.
9. Belah Ketupat memiliki Simetri Putar tingkat 2.
10. Memiliki 4 buah sisi dan 4 buah titik sudut.
11. Keempat sisi belah ketupat mempunyai panjang yang sama.

Rumus yang ada pada Bangun Datar Belah Ketupat

Nama Rumus :

Keliling (K) K = s + s + s + s

K = s × 4

Luas (L) L = ½ × d1 × d2

Sisi (s) s = K ÷ 4

Diagonal 1 (d1) d1 = 2 × L ÷ d2

Diagonal 2 (d2) d2 = 2 × L ÷ d1

Contoh Soal:

Perhatikan belah ketupat di bawah ini!

rumus bangun datar dan bangun ruang beserta gambarnya

Panjang AC adalah 12 cm
Panjang BD adalah 16 cm

Pertanyaannya yaitu:

a. Tentukanlah luas belah ketupat ABCD!
b. Tentukan simak keliling belah ketupat ABCD!

Jawab:

a. Luas belah ketupat ABCD adalah = ½ x d1 x d2, sehingga
= ½ x AC x BD
= ½ x 12 cm x 16 cm
= 96 cm2

Jadi, luas belah ketupat ABCD yaitu 96 cm2.

b. Keliling belah ketupat ABCD adalah: s + s + s + s, sehingga
= AB + BC + CD + DA
= 4 x s
= 4 x 10 cm
= 40 cm

Jadi, keliling belah ketupat ABCD yaitu 40 cm.

Segitiga

Segitiga merupakan suatu bangun datar 2 dimensi yang dibentuk oleh 3 buah sisi yang berwujud garis lurus serta 3 buah sudutSehingga bangun datar yang terbentuk dari tiga atau lebih garis lurus disebut sebagai segitiga.

Sifat Bangun Datar Segitiga

Pada bangunan segitiga, ketiga sudutnya memiliki besaran 180º. (jika dijumlahkan hasilnya 180)
Sifat Segitiga mempunyai 3 sisi serta 3 titik sudut.

Rumus Bangun Datar Segitiga

Rumus luas segitiga.

 Luas = 1/2 x a x t

Rumus keliling segitiga.

 Keliling = sisi a + sisi b + sisi c

Ket :

a = alas
t = tinggi